DIAGRAMMES : SMITH / ROS
Déjà : ROS = SWR (en anglais)
Les anciens ponts de mesure permettaient de mesurer les paramètres d'une antenne, ou plus généralement d'un dipôle (dans le sens d'un circuit présentant deux bornes), à une fréquence particulière; nous dirons incorrectement à fréquence fixe. C'est incorrect dans le sens que l'appareil permettait de changer de fréquence pour faire de nouvelle mesure. Par exemple, on pouvait mesurer le ROS à différentes fréquences et dessiner un graphique avec, en abscisse (horizontalement), la fréquence et, en ordonnée (verticalement), le ROS. Le ROS est une grandeur assez facilement mesurable tans que sa valeur est petite (inférieure à 10). Cette représentation du ROS en fonction de la fréquence est une habitude culturelle et reste significative. Néanmoins je veux montrer qu'elle fait perdre des informations pertinentes en particulier depuis que des appareils de mesures, bon marché, permettent, en une seule opération, d'effectuer plusieurs (beaucoup) de mesures successives dans une bande de fréquence en faisant varier la fréquence pas par pas (incréments) fixés par l'utilisateur. Ces appareils produisent et construise en leur sein une table des mesures en fonction de la fréquence. Cette table permet des affichages sur un écran local ou sur un ordinateur déporté.
A nouveau pour des raisons culturelles (l'avancement des techniques), on a pris l'habitude d'exporter (d'enregistrer) ces données (mesures / fréquences) dans un fichier informatique; les mesures y étant écrites sous la forme des valeurs du paramètre S11. En fait ce paramètre S11 se décompose toujours en deux valeurs qui sont représentatives de l'impédance du dipôle mesurés mais ne sont pas les impédances. Dans l'enregistrement, les deux valeurs ne sont pas toujours du même type en fonction du producteur (appareil de mesure ou simulateur) ce qui peut compliquer le traitement. On aurait pu produire un fichier enregistrant directement l'impédance sous la forme de sa partie résistive et de sa partie réactive mais, pourquoi faire simple quand on peut faire compliqué, on ne l'a pas fait et on enregistre ce paramètre S11 (2 valeurs numériques et la fréquence).
Qu'on se rassure, à partir de la valeur de S11 on peut recalculer la valeur de l'impédance, en ohms résistif et en ohms réactifs. Là aussi, historiquement, on a convenu, sauf conventions contraires explicites, qu'on exprimait cette impédance sous la forme série. Quand on dit que l'antenne (pour une fréquence particulière) fait 75 Ω avec un réactif de -200 Ω on sous entend qu'il s'agit d'une résistance de 75 Ω en série avec une réactance de -200 Ω. Dans beaucoup d'occasion on écrira Z=75 -j 200. Il n'est pas indispensable de comprendre pourquoi on utilise cette lettre 'j' qui est introduite par une théorie mathématique des nombres complexes. On pourrait tout aussi bien avoir une convention d'écriture du genre Z=75; -200 mais on n'a pas choisi cette convention et on peut voir ce 'j' comme un séparateur au même titre que le ';' Expliquer la convention est indispensable car de nombreux appareils et logiciels présentent les mesures sous cette forme 75 -j 200. 75 et 200 sont des ohms Ω. Si la fréquence est de 7 MHz, -200 Ω est la réactance (en Ω) d'un condensateur de 169 pF; notons que si cette réactance était positif ce serait celle, toujours à 7 MHz d'une self de 3,05 µH
C'est quoi S11 ?On a tout compliqué, comme par plaisir de faire compliqué. Le S11 c'est le
coefficient de réflexion et, pour simplifier, on l'a affublé de la lettre grecque gamma Γ; S11 est plus facile à écrire que Γ et j'utilise ici S11 qui est un synonyme. On trouvera dans mon topo :
Un NanoVNA mais c'est très simple le détail des calculs établissant les
formules de conversion mais les voici, brutalement exposées.

Elles sont d'apparences simples mais pas si simples que ça. S11 est un nombre complexe c'est à dire qu'il y a deux valeurs numériques de cachées dans cet unique nombre complexe (comme pour les impédances) :
- L’astérisque '*' indique qu'il s'agit d'un nombre (valeur) complexe. L'algèbre des nombres complexes, addition soustraction produit etc., n'est pas trivial; Excel ou les bibliothèques logicielles en facilitent l'usage.
- |S11| indique qu'il s'agit du module du nombre complexe; c'est un nombre tout simple. Si les deux nombres cachés dans le nombre complexe sont A et B alors |S11| = racine (A²+B²) qui est donc toujours positif
- Z est l'impédance du dipôle; elle est par nature double, résistive et réactive et; on l'a vu représenté par un nombre complexe
- Zc est l'impédance caractéristique de la ligne qui sert de référence, par exemple 50 Ω ou 600 Ω, qui pourrait être raccordée sur le dipôle. Dans le cas général Zc est purement résistive (réactif nul). Le ROS et S11 sont toujours, par définition, exprimés par rapport à cette impédance qui sert de référence (on l'oublie souvent). On en verra des exemples plus loin.
Ce qui faut retenir c'est qu'avec S11* on peut calculer ROS et Z* alors qu'avec ROS,
on ne peut rien calculer du tout.
Rappelons-nous que l'on visualisait le ROS sous forme d'un graphique (voir ci-avant) : ROS fonction de la fréquence. Nous allons nous intéresser à la représentation graphique de ce S11. Le Diagramme de Smith (qui est un gros mot pour beaucoup) est en fait la représentation du S11. Il va par contre être nécessaire d'oublier les vieux réflexes dans l'usage du diagramme de Smith reposant sur un digramme papier avec de multiples échelles graduées et des tracés au crayon. Dans les années 1960, les calculatrices de bureau n'existaient pas et encore moins les ordinateurs personnels. L'abaque de Smith (ou diagramme) remplaçait des calculs fastidieux par des interpolations graphiques. En général, on calculait à fréquence fixe. Ce temps est révolu et le diagramme de Smith n'est plus qu'un simple décor autour de la représentation de S11. En fait, on n'utilise plus l'abaque de Smith donc n'ayez plus peur de M. Phillip Hagar
Smith; on ne conserve que son nom comme celui de M. André-Marie
Ampère.
Pour un dipôle donné (ou prêté

) S11 est fonction de la fréquence (varie avec) mais nous n'allons pas placer la fréquence sur l'axe horizontal du graphique comme pour le ROS. S11 étant un nombre complexe, il intègre en réalité deux valeurs et on va reporter la première valeur sur l'axe horizontal (x) et la deuxième sur l'axe vertical (y). Ce report va définir un point qui sera représentatif du S11 à cette fréquence. La fréquence n'est pas affichée sur le diagramme; c'est un artifice informatique qui nous permettra de connaître la fréquence correspondant à un point de mesure du S11. La valeur du S11 à l'avantage d'être continue avec la fréquence c'est-à-dire que quand la fréquence varie il n'y a pas de saut brusque de la valeur de S11. Il s'en suit que le graphe de S11 apparaît comme une ligne courbe qui a tendance à faire des volutes.
Il est temps de concrétiser ça sur un exemple. Je vais utiliser cette antenne telle que symbolisé dans Eznec:

La simulation est plus simple à mettre en œuvre que la mesure d'une antenne réelle mais les principes rentent les mêmes. J'ai demandé à Eznec de mesurer (évaluer) cette antenne, comme je l'aurais demandé à un NanoVNA pour une antenne réelle, entre 5 et 28 MHz par pas de 5 kHz ce qui représente 4601 mesures. Eznec m'a produit un fichier .s1p représentatif du S11 en fonction de la fréquence. Un NanoVNA ou le logiciel connecté au NanoVNA peuvent produire, eux aussi, ce fichier. Ce fichier je l'ai rendu compatible pour un tracé dans Excel.

Le graphe dans Excel est à droite et en bleu. J'ai ajouté le cercle rouge de rayon 1 parce qu'on démontre que tous les points de tous les graphes d'un S11 sont toujours à l'intérieur de ce cercle. A gauche, c'est une copie de la fenêtre d'un logiciel (nanovna-saver) montrant le diagramme de Smith de cette antenne. On observe :
- Que mon cercle rouge correspond au grand cercle extérieur de l'abaque
- Que ma courbe bleue correspond au graphe brun tracé par le logiciel
- Qu'il n'y a aucune indication numérique sur le graphe produit par le logiciel
- Que sur mon graphe dans Excel les axes portent des graduations de valeur des deux nombres cachés dans le nombre complexe S11
A gauche, on observe un petit triangle rouge. C'est ce qu'on appelle un marqueur et l'utilisateur peut le poser où il le souhaite sur la courbe. Le logiciel affiche alors tout un tas de propriétés qu'il a calculé à partir de la valeur de base de S11
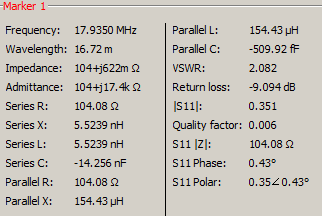
Le logiciel en oublie même de nous donner les valeurs des deux nombres cachés dans le S11 comme je les montre dans le graphe Excel. Le libellé des valeurs affichées par le logiciel nanovna-saver est un casse-tête et il n'y a pas de documentation. Voici les plus simples
- Impedance : montre la valeur de l'impédance du dipôle, partie résistive et partie réactive avec la convention du 'j' séparateur; mΩ veut dire milli ohm
- Serie R : on retrouve la partie résistive de l'impédance en Ω
- Serie X : Ah, ce n'est plus en ohm mais nanovna-saver a calculé la self équivalente aux 0,622 Ω à 17.9350 MHz
- |S11| : la distance entre le centre du cercle et le point, soit le module de S11
Sauf pour faire des calculs particuliers la valeur de S11 n'est d'aucune utilité; c'est la position et la forme de la courbe qui est très intéressante pour y poser le marqueur.
- Les points sur l'axe horizontal correspondent à des impédances dont le réactif est nul c'est ce qu'on appelle les points de résonance et on peut en lire la fréquence en y posant un marqueur.
- Les points au dessus de l'axe horizontal indiquent une impédance avec un réactif selfique
- Les points en dessous de l'axe horizontal indiquent une impédance avec un réactif capacitif
J'ai choisi une résistance de normalisation de 50 Ω car le logiciel nanaovna-saver est adapté aux NanoVNA 50 Ω. L'impédance de normalisation peut être quelconque et Eznec permet de la choisir. Le comparatif ci dessous, colonne de gauche est pour une normalisation à 104 Ω la colonne de droite une normalisation à 630 Ω. La normalisation s'applique au Smith comme au ROS.
 C'est la même antenne à droite et à gauche
C'est la même antenne à droite et à gauche. Remarquez comment le graphe du ROS peut être trompeur. En bas à droite, j'ai ajouté, à la main, les valeurs des fréquences de résonance. Ces fréquences de résonance se retrouvent à droite et à gauche bien que le graphe n'ait pas la même forme. Si on envisage de raccorder une antenne sur une ligne en fils parallèle de 600 Ω pourquoi examiner les mesures normalisées sur 50 Ω.
J'espère que cet exposé aura convaincu certains de regarder déjà le Smith avant de se polariser sur le ROS. J'espère que c'est plus claire qu'une vidéo YouTube.
