Une façon simple et efficace de mesurer l'impédance caractéristique est de disposer d'un échantillon de ligne, relativement court par rapport à la fréquence (genre 1 m pour F<50 MHz). On mesure
• La valeur de la self, la ligne étant en court-circuit, en µH
• La valeur de la capacité, la ligne étant en ouverte, en pF
Alors l'impédance caractéristique Zc = 1000 * racine (LµH/CpF). Mais en BF, pour un câble normal Rdx est important par rapport à Gdx et la valeur de Zc est plus grande que celle en HF où Rdx et Gdx sont masqué par Ldx et Cdx
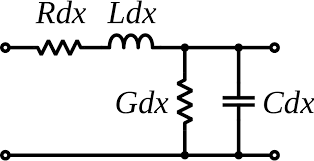
Zc = racine ((R+jLw)/(G+jCw))
D’où l'intérêt de mesurer Zc en HF
Il me semble que
Zc = racine (Zo*Zf)
Zc est l'impédance caractéristique sous forme complexe
Zo est l'impédance complexe présentée par la ligne son extrémité étant ouverte
Zf est l'impédance complexe présentée par la ligne son extrémité étant fermée (en court-circuit)
Avec mon nanaoVNA j'accède à S11 (fichier .sp1) et avec Excel je peux calculer facilement grâce au fonctions COMPLEXE.xxx Zo et Zf (sous forme complexe). Je peux alors calculer Zc et afficher les valeurs en fonction de la fréquence. Ça marche mais ça montre des limites et je ne comprends trop pourquoi

Il s'agit d'une paire constituée par la mise en parallèle des conducteurs en diagonale sur une quarte d'assemblage d'un câble téléphonique Ø 0.6 mm Cu. La première résonance en 1/4 d'onde est à 23.432 MHz (1/2 onde vers 50 MHz). Auriez vous une idée de pourquoi la mesure dégénère au delà de 15 MHz.
J'ai fait la même chose pour un petit câble 50 ohm isolé au téflon

Les résultats interrogent. Comment expliquer ?
